Reference:
Traveling Salesman Problem
Computer Science is no more about computers than astronomy is about telescopes - Edsger Dijkstra
Before we get to TSP lets cover some graph theory and other topics. This post is a bit long but I want to cover some interesting stuffs I noticed.
graph theory
Graphs are consist of nodes and edges. These trivial components set the way for some neat applications using tree operations.
DFS
DAG (Directed Acyclic Graph) utilizes DFS (depth first search) tree traversal. It uses topological sort algorithm to check for depencies such as Git and Mercurial. On a general view, DAQ works by recursively diving into the tree by marking node as visited along with timestamp and continue moving to the next adjacent node and backing out of the branch until all the nodes are visited. If you are lucky and the graph has no cycles, it can be used to find the shortest path better than Dijkstra algorithm. The algorithm is \(O(V+E)\) for traversing each node and edges.
DFS(G) {
for each vertex u in G.V {
u.color = WHITE;
}
time = 0;
for each vertex u in G.V {
if (u.color == WHITE)
DFS_Visit(G,u);
}
} Here an example of using DAG for find the shortest path problem. This requires the few changes: (1) topologically sort the graph abovce, (2) initialize nodes, and (3) relax edges Relax(u,v,w) for the least cost path from u to v. The additional steps adds a constant factor to the run time so it remains as \(O(V+E)\).
Relax(u,v,w) {
if (d[v] > d[u]+w) then d[v]=d[u]+w;
} 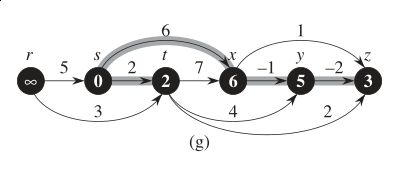
Node marked as visited will appear in reverse topological order and useful in Git where you want to see the most recent commits anyway.
BFS
BFS (breath first search) on the other hand moves through the graph by visiting all the adjacent nodes first but no further before visiting the next set of adjacent nodes. Different algorithm will differ by how it picks the next nodes but the path still represent the shortest path from node A to B. Dijkstra algorithm works in similar way and used in applications such as navigation and network routing. The algorithm result in \(O(V+E)\).
BFS(G, s) {
initialize vertices;
Q = {s}; // Q is a queue initialize to s
while (Q not empty) {
u = DEQUEUE(Q);
for each v in G.Adj[u] {
if (v.color == WHITE)
v.color = GREY;
v.d = u.d + 1;
v.p = u;
ENQUEUE(Q, v);
}
u.color = BLACK;
}
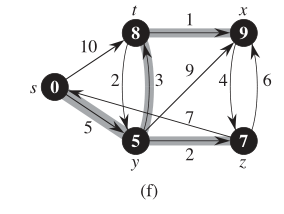
} Here is an example of using Dijkstra algorithm for find the shortest path. A few things must be changed in the above algorithm, (1) edges have different weight \(w\) to reflect the cost and (2) initialize nodes and (3) relax edges Relax(u,v,w) for the least cost edge from u to v and (4) queue is replaced with priority queue. The last two adds quite a bit overhead cost (depeding on the ADT choice) for accessing and updating each node. For array ADT this adds up to \(O(V^2)\).
Dijkstra(G, w, s)
InitializeSingleSource(G, s)
S <- NIL
Q in V[G]
while Q not 0 do
u <- ExtractMin(Q)
S <- S + {u}
for v in Adj[u] do
Relax(u,v,w)
Relax(u,v,w) {
if (d[v] > d[u]+w) then d[v]=d[u]+w;
} 
Why use Relax? It is the greedy approach that gives local optimal solution. Not surprisingly it is also used in finding the minimum spanning tree like Prims algorithm. Unlike Dijkstras algorithm, Prims algorithm is great for finding the minimum weight tree for undirected graph as well. The run time is the same depending on the ADT.
MST-Prim(G, w, r)
Q = V[G];
for each u in Q
key[u] = inf;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v in Adj[u]
if (v in Q and w(u,v) < key[v])
p[v] = u;
DecreaseKey(v, w(u,v)); P vs NP
Can we solve the TSP problem now? Not quite. In the graph theory portion, we have seen many variation of single source shortest path problems and they can be solve in polynomial time by examining the Big-O run time limits. TSP does not fall into that category, it belong to the non-deterministic polynomial, specifically NP-Complete. TSP is finding the shortest path but it can only visit each place once. The figure below shows how problems in many scientific and engineering field can be polynomially-reduced to TSP. While no algorithm exist yet or proof for P=NP we can use the next-best thing Approximate algorithm while David X. Cohen and Jeff Westbrook fight it out in my imaginary world where Futurama is still running.
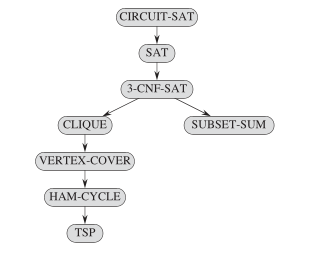
iterative Improvement
This brute force method is used to improve an approximate tour given by greedy or nearest neighbor algorithm. The key is to break the tour in two positions and swap the two ends. A successful iteration would eliminate the knot and improve the approximate tour. This can be used along with any algorithm.
- A B - - A - B -
X ==>
- C D - - C - D -Nearest Neighbor Algorithm
The NN algorithm is one of the simplest to implement. It starts with a random vertex and continue picking the closest point or least cost vertex and add it to the TSP tour until every vertex is added.
This algorithm was implemented due to simplicity and speed. The problem is that it doesn’t guaranteed lower bound and may not even find optimal tour if there is one. This, however, can be improved using 2-optimization or 3-optimization iterative algorithm.
Pseudocode
1. start on an arbitrary vertex as current vertex.
2. find out the shortest edge connecting current vertex and an unvisited vertex V.
3. set current vertex to V.
4. mark V as visited.
5. if all the vertices in domain are visited, then terminate.
6. Go to step 2.Christofides Algorithm
The Christofides algorithm is one of the best algorithm to find an optimal tour at 3/2-approximation. The algorithm utilizes the minimum spanning tree and combines with minimum weight perfect match edges to form the Euler circuit. The near optimized Hamiltonian circuit can be derived from this process.
Let C be the optimal tour. The minimum spanning tree T includes the edges in C and removing one edge to form the tree. So, \( w(T) \leq w(C) \). Next, O is the subset of vertices of odd degree can be used to find the minimum-weight match M. The set M contains edges that contains at most half of all edges found in C: \( w(M) \leq w(C)/2 \). The combined circuit and the approximate tour is therefore less than:
$$ w(T) + w(M) \leq \frac{3}{2}w(C) $$ or $$ w(TSP) \leq 1.5w(C) $$
The advantages of Christofides algorithm is that it guarantees how close the approximation will be compared to the optimal solution. The downside is that finding the minimum spanning tree can become a bottleneck in the implementation as we have found. This means that solving problems with moderate input size will take a while.
Pseudocode Create a minimum spanning tree T of G. Let O be the set of vertices with odd degree in T. By the handshaking lemma, O has an even number of vertices. Find a minimum-weight perfect matching M in the induced subgraph given by the vertices from O. Combine the edges of M and T to form a connected multigraph H in which each vertex has even degree. Form an Eulerian circuit in H. Make the circuit found in previous step into a Hamiltonian circuit by skipping repeated vertices (shortcutting).
The following result is achieved by implementing the nearest neighbor and continuously improving the tour through iterative algorithm for 3 mins
input | Best result | Time | Optimal solution
------------- | ----------- | ------ | ---
tsp_example_1 | 110,484 | 3 mins | 108,159
tsp_example_2 | 2,999 | 3 mins | 2,579
tsp_example_3 | 1,946,282 | 3 mins | 1,573,084